4.Allan偏差

       对数——对数图的使用仅仅解决了“计算”部分中描述的一个问题。另一个问题——方差的单位为“平方”，这使我们无法解释对数——对数图曲线上对应的Y值的概念。

       为了解决这个问题，我们可以使用Allan偏差（标准偏差或标准差）而不是Allan方差。偏差是方差的平方根，因此要从Allan方差中得出Allan偏差，只需取上面计算出的每个方差的平方根即可。这会将数据单位改回我们可以直观理解的单位（即传感器实际记录的单位——加速度单位）。

       但是，标准偏差的含义比方差要更难理解一点。方差是数据集合的整体分布统计，而标准差只是数据中与平均值接近的68％的数据的分布统计。比如，如果平均值是0，而标准偏差是正负5，则该数据集的大约32％大于5且小于-5。因此，方差告诉你highest和低范围，标准差仅告诉你大部分数据位于何处。

       也就是说，偏差图更一目了然。

       我们可以通过计算Allan方差的平方根，然后得到如下的Allan偏差图： 

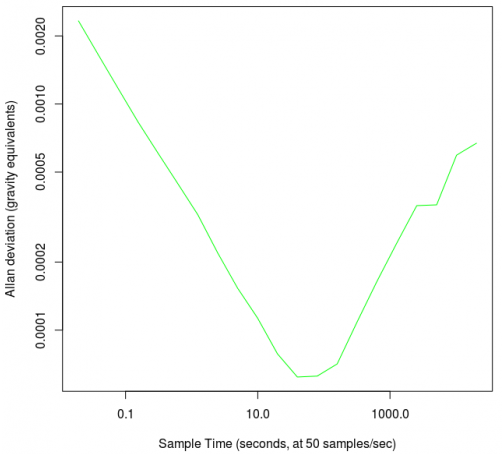
5.如何使用Allan偏差图

       使用Allan偏差图比较产品或学习如何使用传感器时，可以将图中的曲线分为四个部分。当然网上还有其他有关如何解释这些图的教程。为了将不同类型噪声的影响分开，其中一些教程将Allan偏差图分成了更多部分。对于此处的实际讨论，我们省去了有关不同类型噪声的许多细节。常见的Allan偏差图的四个部分如下：

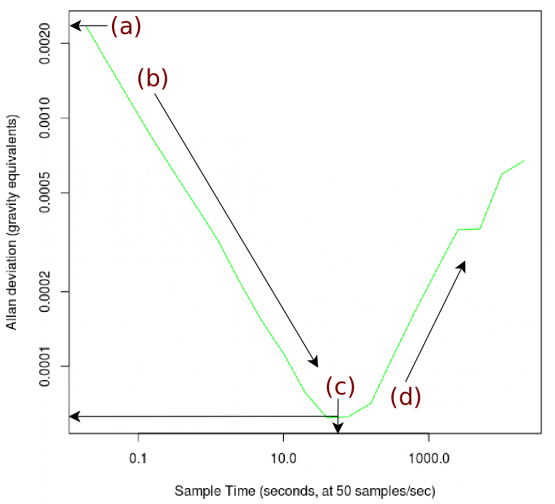
我们将在下面更深入地讨论所有这四个部分：

A点——对应的Y值是任何一次测量的噪声的标准偏差，或者以单个数据点间隔为平均时间的噪声。

B段——表示随着平均时间的增长，平均值标准偏差逐渐减小，可用于校正快速波动的噪声。

C点——终，通过延长平均时间，噪声可以达到一个小值。该小值具有用户感兴趣的optimal平均时间X和小系统噪声（或信噪比为1时的灵敏度）Y值，C点也就是前文提到的“大信噪比”所需的平均时间。

D段——在较长时间范围内的慢变噪声或系统漂移占主导，开始影响较大组的平均数据。

5.1. A点——单点噪声

       Allan偏差图的起点是单个点的噪声标准偏差。因为在图的开始处， “组”的大小为1。因此，组与组之间变化的标准偏差将等于各个点的标准偏差。因此，通过对比所计算数据集的起始Allan偏差和各个点的标准偏差，可以初步确认Allan偏差计算的准确性。

       请注意，对于偏差（漂移）不大于白噪声的情况，上述描述是正确的。如果偏差随时间的漂移比短时间内白噪声产生的漂移大，则数据集的标准偏差将是测量偏差，而不是白噪声标准偏差。

用于选择产品

       在比较产品时，A点数值对需要尽可能少的平均数据的应用场景有很大价值。即，用户需要尽可能多的使用每个数据点，或者需要尽可能多的保留数据中的高频分量。对于大多数应用，如“噪声”部分所述，至少进行一些平均是非常有用的。

实际应用

       使用传感器时，此值在尝试评估单个测量点的噪声时很有用。大约68％的测量结果将产生0.0025g的噪声误差，而32％的测量结果将具有更大的噪声误差。正如“噪声”部分中所述，要确定单个测量数据点的噪声是大是小，是正是负，实际上是不可能的。因此，将A点数值与你期望获得的测量值幅度进行比较，以及噪声误差是否会成为测量数据的重要分量，会对实际应用非常有帮助。

5.2. B段——通过平均来改善精度

       随着你可以收集越来越多的数据，并将它们取平均，你可以对数据进行精度更高的提取。

用于选择产品

       要使用从A点的大值到C点的小值的B段区间，你需要考虑自己的应用场景。你可以合理采样和平均的时长是多少？你是否想要每0.1秒获取读数或每1秒一次获取读数？如果你的应用试图在Allan偏差图中测量相对于噪声非常小的信号，则需要在可平均的时间范围内，比较不同产品的Allan偏差图。

实际应用

       在可允许的采样运算时间内，通过调整平均时间的长度，抑制每单位时间的降噪量，优化系统的信噪比，同时保证系统足够的响应速度，可以帮助你更准确的微调应用场景中的数据采样和平均时间间隔。

       例如，在很多四轴飞行器的应用中，通过适当平滑加速度计的输出数据，以抑制其跳跃性的噪声，可以帮助你更准确地估计GPS读数之间的飞行器位置。对于加速度数值远大于噪声的情况而言，平均可以稍微平滑这些噪声，但不会影响加速度计输出结果的准确性。因此，只要你感兴趣数据的价值足够大，且平均时间足够长而不会受到太大影响，则可以收集到更多的数据样本来更有效地过滤噪声。这种偏差建模——通过延长平均时间法——允许你沿着B段斜率向下移至一个系统可接受的响应平均时间的小值。

       但是，对于测量比采样频率更快的振动信号，这种方法将不再起作用。

5.3. C点——小偏差（optimal灵敏度）

       理论上，此小偏差是传感器的optimum精度。实际应用中，即使要达到这一水平也可能是很困难的。为此，你必须以约等于小C点的平均时间处理数据。这需要非常特定的应用程序和采样策略。

       对于例子中的加速度传感器，optimum灵敏度大约是每100秒平均一次，每秒50个采样，也即采集5000个点平均一次获得的。请记住，optimum灵敏度只是噪声的标准偏差，因此，即使在C点的输出，也将有大约三分之一的噪声大于图中显示的小值。

用于选择产品

       Allan偏差图上的optimal灵敏度值，是比较不同传感器常用的特征点。该数据点的用途是向你显示灵敏度optimum的情况。根据Allan偏差图，你可以选择采取不同的采样时间，并且在所需的灵敏度上有多少回旋余地（平均会大大提升传感器的灵敏度），但请记住，你的数据仍会在C点小值附近产生偏差。事实上，在选择产品时，图形上的所有点都具有价值的。

5.4. D段——低频噪声

       当你在此低频噪声中仅取一小部分值（例如随机噪声）时，数值变化会非常小。在越来越大的数据组中，随机噪声可能会很大。该噪声通常是多个因素的叠加，包括温度的影响，振动和随机游走等。

       像其他噪声一样，真正随机噪声终将平均为零。但是，你将必须收集非常非常长时间的数据。足够长的时间可以保证你的数据捕获任何合理的重复频率的随机噪声。但是，想象一下——假设你发现新的小噪声点超过了数万秒的平均时间——你是否真的想对所有这些数据进行平均以确定小偏差？这样做，你会错过所有来自传感器的真实，快速的数据，因为你一直都在等待采集足够的数据做长期平均值。

用于选择产品

       即使要在曲线的较早一点进行平均，该图的这一部分仍然非常重要。这是由于这样的事实，无论平均周期如何，你仍然会经历随机或温度依赖形式的低频噪声。想象一下，一组1000个数据点的中值在整个过程中缓慢漂移。如果将每十个数据点平均一次，则可能会减轻大部分白噪声，但数据仍将漂移至以前相同的量。

       在Allan偏差上做一个与X轴平行的直线，该线与Allan偏差曲线交于e和f两点，如下图所示。e点和f点虽然平均时间不同，但是检测精度其实是相同的。如果这个Allan偏差曲线右端对应的Y值高于左端first的Y值，说明到达此点时间后，系统已经漂移超过原始未平均的灵敏度。

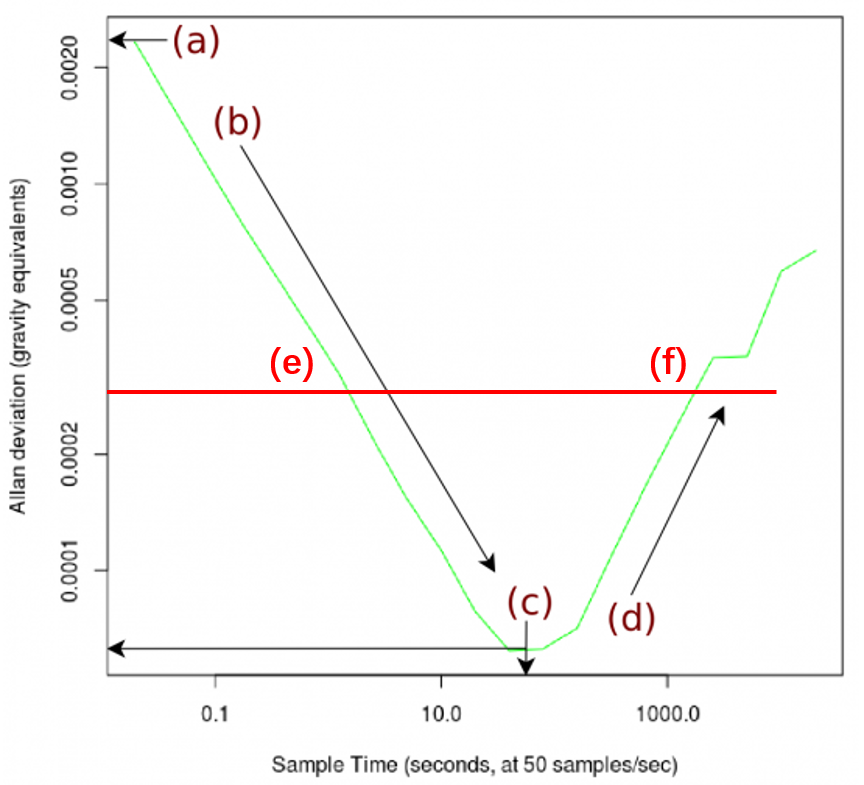
       如果你对传感器和所收集的数据有非常清楚的了解，则可以使用软件算法校正和处理低频噪声，但这是很困难的，只能根据具体情况进行。如果这种操作在你的应用中不可行，则选择低频噪声曲线较浅的传感器将很有价值。当然，你会发现传感器的低频噪声与传感器的成本直接相关。

6.温度的影响

       当温度变化时，电子系统会经历一定程度的误差变化（温飘），终反映在噪声特性中。当查看加速计数据随时间变化时，这些温度影响并不是立即显而易见的，例如“测量噪声”部分中的图形。

       但是温漂效应和其他较小的难以控制的影响使惯性导航变得极为困难。如果在室温下记录加速度计的Allan偏差图，则低频噪声特性（曲线上的D段）可能不会非常陡峭。但是，如果你使用相同的加速度计并将其置于动态温度环境中，则会发现低频噪声曲线将变得更加陡峭或难以预测。通过比较这两个Allan偏差图，并使所有其他变量保持恒定，你可以大致确定温度变化对设备的影响有多大。